Building an AI-generated Pong
What if we give lots of screenshots from a game to a neural network and let it dream its own version?
I recently found out about Oasis, an AI-generated Minecraft clone. You can actually play it right now from your browser, and I encourage you to do it! What you will see is entirely AI-generated: you select a world (which is just a screenshot of a scene) and then the following frames are entirely generated by a neural network.
Roughly, my guess is they gathered lots of gameplay data and trained a model to predict the next frame given the current frame and user input. Once the model is trained, it can be used as some sort of “game engine” by just feeding a screenshot of the game. Then, the neural network will start generating the next frames conditioned on our input.
I find this idea fascinating: we are replacing all the game/code logic by a neural network that has been only trained on image data.
The idea of this blog post is to log my adventure into learning and (hopefully) building a similar AI-generated game engine. As an experiment, I wanted to make this public since the start so that I commit to it. However, expect this to be a little bit messy at first!
World Models
If we want to build a similar AI-generated game, the first thing to do is to look into the literature. I found out that Oasis is powered by a world model [1], whose task is to predict the next state of the world given the previous state/s and action/s. You can find quite a lot of papers related to world models, as well as technical info about Oasis [2].
However, I think that it is important to not overcomplicate things when building something for the first time. In this specific case, it implies (i) avoiding models/techniques that require a huge amount of computing (e.g. training a ViT on lots of Minecraft gameplay) and (ii) avoiding super complicated techniques that provide marginal increases in performance. In other words, adding a complicated training scheme to improve performance by 2% may be essential when building an actual product, but if we want to learn, we should get away with the simplest solution.
I think that IRIS [3] is a good candidate, as it is relatively simple, it works on small Atari games requiring small amounts of data and I think that it is also being used in production at comma.ai.
Also note that most of the papers that talk about world models are related to Reinforcement Learning (RL). The main idea of all those papers is that RL agents are extremely sample inefficient, so it might be a good idea to learn a world model of the environment that can then be used to train the RL agent in its own “imagination”. Most papers follow a scheme of (i) gathering observations from the environment (ii) training the world model (iii) training the RL agent with the world model. In our case, we are only interested in the second step, while the RL agent is just used to gather data from the environment (instead of us having to play for hours to gather data). In other words, we actually don’t care that the RL agent performs well, we just want to have a decent world model.
IRIS
Let’s look at the diagram below. We have the following components:
-
A discrete autoencoder composed by the encoder \(E\) and decoder \(D\). \(E\) is used to convert a frame into a set of \(K\) tokens \((z^1, z^2, ..., z^K)\), whereas \(D\) is used to reconstruct the original image from the tokens. Why is this required? Because we are going to use a transformer as the actual “engine”, and it only works at the level of tokens. Notice that we could treat each individual pixel as a single token, but as mentioned in the paper, the attention mechanism grows quadratically with the sequence length so this is unscalable.
-
A transformer \(G\) to predict the next state of the environment. It receives sequences of consecutive frame/action tokens \((z_0^1,...,z_0^K,a_0,...,z_t^1, ...,z_t^{K})\)
-
A policy \(\pi\), that will be used to select the action given the previous states. Obtaining a good policy is the main objective of the paper, but we actually care about properly modeling the game.

IRIS diagram. Source: [3]
Once that world model is trained, we will feed the initial frame to the encoder to obtain the initial tokens \((z1_0,...,zK_0)\). Then, instead of sampling the action from the policy, we will retrieve it from the actual user, then use GPT to generate the tokens of the next state, and then decode them to obtain the next frame.
That’s cool but, how do we actually train?. Essentially, each training step consists of three different processes:
- Collect experience: Use the current policy to play the actual game and gather experience.
- Update the world model: Use the previous experience to train \(E\), \(D\) and \(G\) to properly predict the next observation, as well as the rewards and episode end.
- Update the behavior: Improve the policy and value functions in the world model.

IRIS algorithm. Source: [3]
Getting our hands dirty: AI-Generated Pong
Instead of having to figure out everything before coding, let’s get our hands dirty by trying to get a minimal working implementation. My idea is to first take a simple game (such as Pong) and try training a world model with just a random policy. In other words, this means gathering data from games where the policy is just “move up/down/do nothing with 33% probability” and train the world model with that data. Then, we can think about actually including RL.
- Setup Pong
- Implement VQ-VAE
- Implement GPT
- Train the world model on gathered eperience and visualize it.
- Interact with world model
- Come up with a better policy?
1. Setting up Pong
We are going to use Gymnasium, a maintained fork of OpenAI’s Gym RL library. This library is really convenient as it already has implemented all the common RL environments, including Pong and other Atari games. Setting up Pong is really easy:
import gymnasium as gym
import ale_py
gym.register_envs(ale_py) # optional, helpful for IDEs or pre-commit
env = gym.make("ALE/Pong-v5", render_mode="rgb_array")
# Reset the environment to start
observation, info = env.reset()
frames = [observation]
# Run a random action loop
for _ in range(1000):
action = env.action_space.sample() # Choose a random action
observation, reward, done, truncated, info = env.step(action) # Take a step
frames.append(observation)
if done or truncated:
observation, info = env.reset() # Reset the environment if done or truncated
env.close() # Close the environment
import cv2
out = cv2.VideoWriter('pong.avi', cv2.VideoWriter_fourcc(*'XVID'), 30, (frames[0].shape[1], frames[0].shape[0]))
for frame in frames:
out.write(cv2.cvtColor(frame, cv2.COLOR_RGB2BGR))
out.release()
The snippet above creates a Pong environment with gym.make and starts it with env.reset(). This function returns observation, which is a (210x160, 3) RGB array of the screen, and info about the environment. Then, for 1000 steps, it randomly selects an action and executes it inside of the game, obtaining the next observation of the environment, as well as the reward for taking the action, whether the agent reaches terminal state (done), and whether the execution has reached its limit (truncated). The last part of the snippet is just used to save a video of the simulation.
12 games played by our random agent. It is recommended to watch it on fullscreen.
As you can see, our random strategy leaves a lot to be desired: looking at the 12 episodes shown above, you can see that it struggles to bounce the ball back (altought it surprises me that it is able to score two points in some episodes lol). This implies that the data collected from this random agent will leave out a lot of the game logic (e.g. the dynamics of the ball, the green score counter) that the world model will not be able to, well, model.
In other words, we should expect that a world model trained from the random agent experience will properly model the movement of our player, and maybe the first collision of the ball, but the other mechanics will be undefined as it hasn’t seen any data about them.
For now, we are going to implement the actual world model, train it with the experience of the random agent, and test whether this is true or not. Then, we will actually implement a proper RL agent.
2. Implement VQ-VAE
Before explaining the VQ-VAE, it is a good idea to think about where it comes from. The VQ-VAE is basically a version of the good old autoencoder.
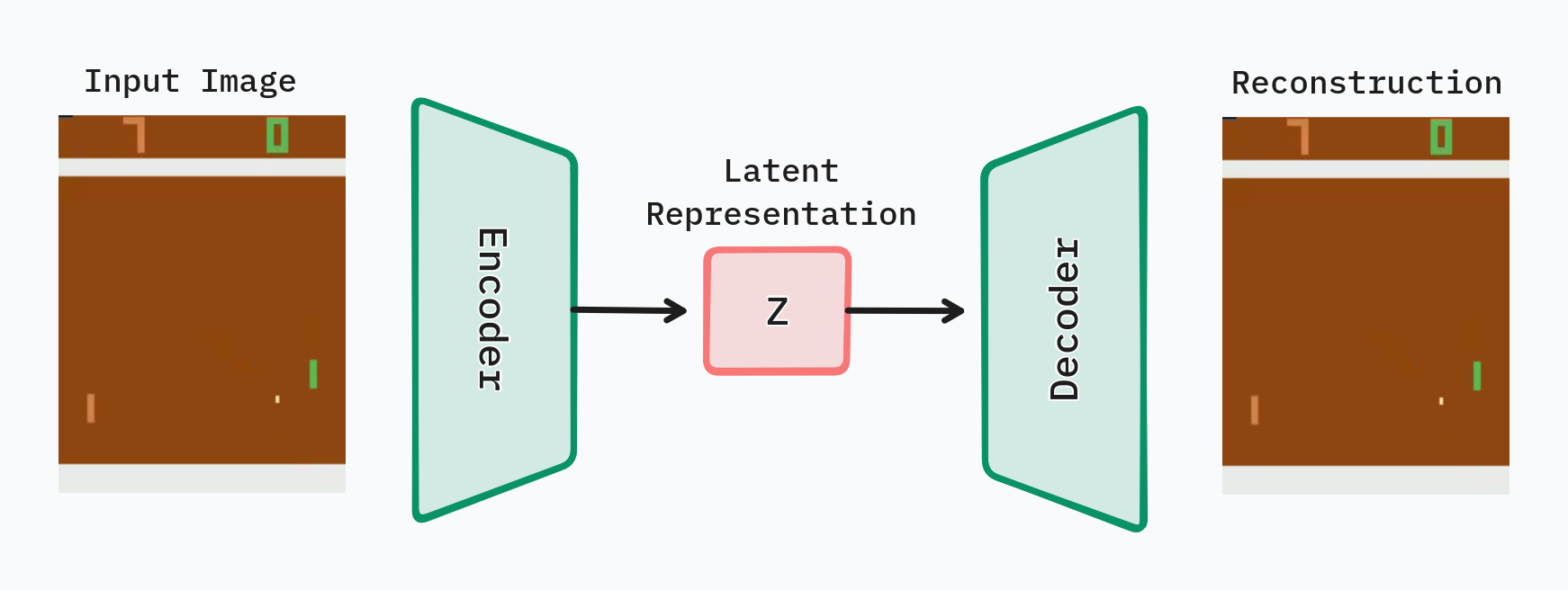
The autoencoder is composed by two components:
- An encoder, which maps the input (in our case, a frame image) into a latent space vector \(z\).
- A decoder, which takes the latent vector \(z\) and tries to reconstruct the input from it.
The main idea here is that by training an autoencoder to reconstruct the input images, it will also learn good representations in the latent space. Then, these representations can be really useful for several applications such as compression, image generation or anomaly detection.
In our specific case, why do we want to use autoencoders? We want to build a world model that, given the current frame and action, generates the next frame. More specific, the backbone of the world model is going to be a transformer that takes all the previous frames and actions and generates the next frame. The thing is that directly feeding images to the transformer is going to be unfeasible as the computational cost of the transformer grows quadratically with the number of frames. Therefore, the idea is to compress the frames into a smaller latent representation via an autoencoder.
We are going to use a variation called Vector Quantised-Variational AutoEncoder (VQ-VAE). Don’t worry about the name, this is simply an autoencoder. The main difference is that the latent space is discrete instead of continuous. In specific, we will have a dictionary of possible latent vectors \(D = {e_1, e_2, ..., e_N}\) and the output of the encoder will be encoded into the nearest of these vectors, \(z_q = \mathcal{E}(z) = \arg\min_{e_i \in D} \| z - e_i \|_2^2\). The training loss will be:
\[\mathcal{L}(E,D,\mathcal{E}) = \|x - \hat{x}\|_1 + \|\text{sg}(z) - z_q\|_2^2 + \|\text{sg}(z_q) - z\|_2^2 + \mathcal{L}_{perceptual}(x, \hat{x})\]where \(\hat{x} = D(\mathcal{E}(E(x)))\) is the reconstructed input, and \(\text{sg}(\cdot)\) is the stop gradient operator. We have four loss terms that enforce different things:
- The first term is the reconstruction loss. It encourages the autoencoder to output an image similar to the input.
-
The next two terms form the commitment loss. These terms are included to ensure that the dictionary is actually learned. It was difficult for me to understand the motivation behind the commitment loss, but the explanation given by Claude was helpful:
“Imagine you’re playing a game where you need to stand close to one of several fixed points on the ground (these are like your codebook vectors). But instead of moving yourself to the nearest point, you could technically just walk further and further away from all of them. There’s no rule saying you can’t do that - but it defeats the purpose of the game!
This is essentially what could happen with the encoder. Without the commitment loss, the encoder parameters might update in a way that keeps pushing its outputs further from the codebook vectors, rather than learning to produce outputs that are close to them. This would undermine the whole point of vector quantization, which is to learn a discrete representation.”
- Finally, the last is a perceptual loss, included to encourage the autoencoder to generate images that are perceptually similar to the input images. In the original IRIS repo, they use the LPIPS loss.
For the implementation, I will mostly borrow it from the commaVQ repo as it is clear and simple. I will also look at the original IRIS repo for details about the hyperparameters, loss terms, etc.
import torchvision.transforms as T
transform_ = T.Compose([
T.ToTensor(),
T.Resize((64, 64)),
])
# `observation` is a (210, 160, 3) RGB image
# x has shape (batch_size, c, h, w) = (1, 3, 64, 64)
x = transform_(observation).unsqueeze(0)
config = CompressorConfig()
encoder = Encoder(config)
z, z_q, indices = encoder(x)
print(f"{x.shape=}, {z.shape=}, {z_q.shape=}, {indices.shape=}")
> x.shape=[1, 3, 64, 64], z.shape=[1, 16, 512], z_q.shape=[1, 16, 512], indices.shape=[1, 16]
decoder = Decoder(config)
x_hat = decoder(indices)
print(f"{x_hat.shape=}")
> x_hat.shape = [1, 3, 64, 64]
The snippet above shows how the input is transformed by the different components of the VQ-VAE. We initially have an observation of the environment, represented by an array of ints in the range [0, 255] of shape (210, 160, 3). It is first transformed into a torch tensor of floats between [0, 1] and shape [1, 3, 64, 64], where the first dimension is just a “dummy” batch dimension. The encoder then outputs three variables.
The first one, z, is the raw output of the encoder, and has shape (b, hz*wz, z_channels), where z_channels=512 is the token embedding dimension drawn from Table 2 of the IRIS paper, and hz/wz are the downsampled spatial dimensions (hz = h // 16). In other words, our observation, instead of being represented by an RGB array, is instead represented by 16 vectors of size 512.
However, these vectors are still continuous. But we want to use GPT, a transformer architecture, that actually works with discrete tokens! This is why we use VQ-VAE: z_q is the result of taking the vectors from the dictionary that are closest to the ones in z, and indices contains the actual indices of each token. Put differently, we now have a fixed dictionary represented by a matrix emb of shape (dictionary_size, z_channels). For example if indices=3, then z_q = emb[3].
Finally, the decoder takes the indices that represent the initial image and outputs a reconstruction of it.
Cool, now that we have gained a little bit of intuition about how the VQ-VAE works, it is time to get to work and train it. The idea here is to gather a lot of frames from Pong and train the VQ-VAE to reconstruct them. It should act as a sanity check to ensure that we have properly implemented it before jumping into the next step, which is to implement the GPT architecture that will be actually used to model the game dynamics.
Lesson learned: First, I tried training the autoencoder with just the reconstruction and commitment loss (i.e. no perceptual loss). I found that the autoencoder was able to reconstruct the “background of the game” but struggled to reconstruct small but essential details such as the paddles, the ball and the score counters. It turns out that this is the main motivation behind including a perceptual loss: while the reconstruction loss compares at pixel level, we also need to focus in a way that aligns more closely with human perception. In other words, the autoencoder is able to reconstruct most of the pixels, resulting in a small reconstruction loss, but in reality it misses the most important parts of the game! That’s why we need to include something like a perceptual loss.
Lesson learned 2: I was getting the same (bad) reconstruction for every image. This was caused by how I was handling the vector quantization, i.e., the jump from z to z_q. Initially, what I did was to direclty feed z_q to the decoder. However, this breaks the computation graph, completely ignoring the encoder during training. What the authors of IRIS do, is simply the following:
decoder_input = z + (z_q - z).detach()
Which, expressed in words could be translated as: take the quantized vector in the forward pass, but keep the original gradient during the backward pass.
The video below shows 10 random frames in the top row and their corresponding reconstructions over the course of training. You can actually see how the autoencoder learns how to reconstruct different aspects of the image in increasing difficulty: first the brown background and white horizontal bars, then the paddles, then the ball and the counter.
3. Implement GPT
Cool! We now have an encoder that transforms a frame of the game into a 16 token representation, as well as a decoder that builds images from these tokens representations. This means that we can now use GPT to model the actual dynamics. In other words, our “AI engine” is going to work on a token space, whereas the user will see the images converted from these token space by the decoder.
To recap, an actual game can be modeled as a sequence of the initial frame, the action performed by the user/agent, then the next frame, etc:
\[(x_0, a_0, x_1, a_1, ..., x_t, a_t)\]Now we would like to train a neural network to autorregresively generate frames conditioned on the actions:
- The game starts \((x_0)\).
- The user performs an action \(a_0\).
- The neural network predicts the next frame \(x_1 = G(x_0, a_0)\).
- The user performs another action \(a_1\).
- The neural network predicts the next frame \(x_2 = G(x_0, a_0, x_1, a_1)\)
- Repeat.
For this, we are going to use a Transformer-based architecture, specifically a GPT model. Yes, this is essentially has the same structure than the actual models used on ChatGPT, but way smaller and trained with way less data. But before starting to implement GPT, you might be wondering: why do we need the autoencoder? Can’t we just train GPT on plain images?
Technically, you could. A frame is represented by a (64, 64, 3) array of integers between [0, 255], so you could represent an image by a sequence of 64*64*3 = 12288 tokens, i.e. the sequence would be something like \((x_0^1, x_0^2,..., x_0^{12288}, a_0, ...)\).
The thing is that the cost of the attention operation (which is the backbone and the main mechanism behind the success of Transformer models) grows quadratically with the sequence length. As a comparison, people are currently running models with ~8k tokens of context length. Also, this representation is really inefficient as images are extremely redundant: instead of representing all the pixels of the background, we could say that the background is brown. With the autoencoder, we have proved that all the relevant information of the frame can be encoded into 16 tokens, which is a way more reasonable number.
Now, let’s get to work. First of all, we’re going to focus on what will be the input to the Transformer. Below we can see a dummy example of the input data representing 20 frames of the game:
import einops
from vqvae import Encoder
encoder = Encoder()
batch_size = 4
indices = []
for _ in range(20):
img = torch.rand(batch_size, 3, 64, 64)
_, _, frame = encoder(img) # (batch_size, 16)
action = torch.randint(0, 3, (batch_size, 1))
action += 512 # offset the action indices so that they don't overlap with the frame tokens
indices.append(torch.cat([frame, action], dim=1))
indices = torch.stack(indices, dim=1) # (batch_size, 20, 17)
indices = einops.rearrange(indices, "b l k -> b (l k)") # (batch_size, 20*17)
embedding = nn.Embedding(num_embeddings=512+3, embedding_dim=256)
x = embedding(indices)
transformer = Transformer(TransformerConfig())
y = transformer(x)
print(f"{indices.shape=} {x.shape=}, {y.shape=}")
> indices.shape=[4, 340], x.shape=[4, 340, 256], y.shape=[4, 340, 256]
Let’s get through the example step by step. First, we generate a dummy batch of images which would represent a frame of the game. Then, we pass them through the encoder to obtain the indices of the vector that encode such frames. Then, we take a random action and offset its value by 512 (this will become clearer later). This leads us with a tensor of shape (batch_size, 20, 17). Then, we flatten it to obtain a sequence of tokens representing frame0+action0+frame1....
Finally, this will be the input to the Transformer. The reason why we have previously added an offset to the action tokens is so that they don’t get confused by frame tokens when embedding. Put it another way: if we see a 0 in the sequence, is it the 0th vector of the tokens representing an image, or is it the 0th action? To avoid this confusion, we add the length of the vocabulary of the decoder to the index of each action.
And that’s it! The actual model will also have positional embeddings and a final projection layer to obtain the logits of the tokens from the vocabulary. But the most important thing to note is that this model will take sequences of (batch_size, 20*17) and will output a tensor of shape (batch_size, 20*17, 512+3) representing the logits of the next token prediction. The model will be simply trained to predict the next token via cross entropy loss, and will be trained jointly with the VQ-VAE.
Once that the GPT model has been implemented, our goal is to properly train both the VQ-VAE and GPT. Then, we will save the trained models and check whether it has learned a world model or not.
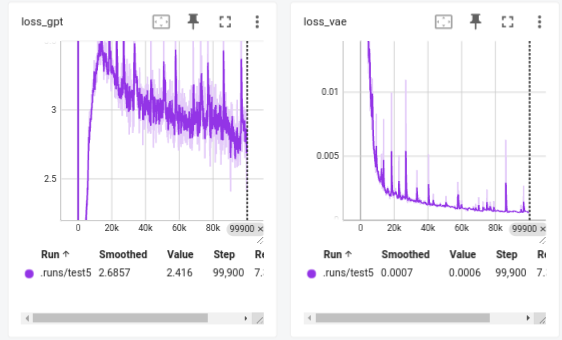
Losses of GPT and VQ-VAE during training.
After ~7h of training, it looks like we could train for a little bit longer but I’m going to begin with the visualization aspect in order to check what it has learned, and whether it already works as a game engine or not. Also, the GPT loss curve does some weird thing where it initially drops by quite a lot, then increases abruptly, and then it steadily goes down. My guess is that, as we’re jointly training both the VAE and GPT, initially the VAE may incorrectly model the images with a small number of vectors, which can then be easily modeled by GPT, hence the lower loss. Then, as the VAE learns to encode the images with a more diverse set of vectors, it becomes harder for GPT to model the sequence.
4. Visualize the World Model
=== UNDER CONSTRUCTION ===
References
[1] https://worldmodels.github.io/